Get premium membership and access revision papers with marking schemes, video lessons and live classes.
Form 3 Mathematics Paper 1 End of Term 2 Exams 2021
Class: Form 3
Subject: Mathematics
Level: High School
Exam Category: Form 3 End Term 2 Exams
Document Type: Pdf
Views: 1119
Downloads: 64
Exam Summary
1. Evaluate
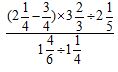(3mks)
2.Use square roots, reciprocal and square tables to evaluate to 4 significant figures the expression; #(0.06458)^(1/2)+ (2/0.4327)^2# (4mks)
3. Three similar 21 inch television sets and five similar 17 inch television cost Ksh.129,250. The difference between the cost of two 21inch television sets and four 17inch television sets is Ksh. 22,000. Calculate the price of a 21- inch television set and that of 17-inch television set. (3mks)
4.Simplify: (3 marks)
# [(a^3- (ab)^2)/(a^4- b^4 )]^(-1)#
5. Solve for x in the equation. (3 Marks)
#9^((2x-1) )times 3^((2x+1))= 243#
6. A classroom measures ( x + 2) m by ( x – 5)m. If the area of the classroom is 60#m^2#. Find its length. (3 mks )
7.A tourist exchanged X US dollars for Kenya shilling when he arrived in Kenya. He spent three days in the country and paid Ksh 45,600 for expenses. He later left the country and exchanged the remainder back to US dollars. He went back with 1200 dollars. Find the value of X to the nearest dollar.
Buying 1 US dollar = Ksh.98.36
Selling 1US dollar = Ksh.98.54 (3mks)
8. Three similar pieces of timber of length 240cm, 320cm and 380cm are cut into equal pieces. Find the largest possible area of a square which can be made from any of the three pieces. (3mks)
9.A regular polygon is such that its exterior angle is one eighth the size of interior angle. Find the number of sides of the polygon. (3 mks)
10.Given that #sin (2theta + 30) = Cos (theta - 60)#. Find the value of tan #theta# to two decimal places. (2 mks)
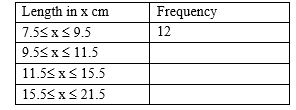
11.The figure below shows a histogram.
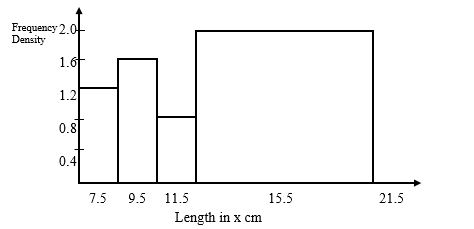
Fill in the table below the missing frequencies. (3mks)
12. A straight line #L_1# is perpendicular to another line #L_2# whose equation is 3y+4x=12. If the two lines meet at point P which lies on the x-axis, find:
(i) The co-ordinate of point P (1mk)
(ii) The equation of line #L_1# in the form y=mx+c (3mks)
13. The heights of two similar pails are 12cm and 8cm. The larger pail can hold 2 litres. What is the capacity of the smaller pail? Give your answer to 2 decimal places. (3mks)
14.Two matrices A and B are such that A= #((k,4),(3,2))# and B = #((1,3),(3,-4))# Given that the determinant of AB = 10, find the value of k. (3mks)
15.#1000cm^3# of milk was shared by three children, Nick, Soita and Swalleh in the ratio #1/4: 1/2 : 1/5#,What volume did Soita get: (2mks)
16. Given that log a = 0.30 and log b = 0.48 find the value of #log b^2/a#. (2 mks)
SECTION II
Answer any five questions in this section.
17.The distance between two towns A and B is 760 km. A minibus left town A at 8:15a.m and traveled towards B at an average speed of 90km/h. A matatu left B at 10:35a.m and on the same day and travelled towards A at an average speed of 110km/h.
(a)(i) How far from A did they meet? (4mks)
(ii) At what time did they meet? (2mks)
(b) A motorist starts from his home at 10:30 a.m on the same day and traveled at an average speed of 100km/h. He arrived at B at the same time as the minibus. Calculate the distance from B to his home. (4mks)
18.The coordinates of a triangle ABC are A(1, 1) B(3, 1) and C (1, 3).
(a) Plot the triangle ABC. (1 mark)
(b) Triangle ABC undergoes a translation vector #((2),(2) )#. Obtain the image of A' B' C ' under the transformation, write the coordinates of A' B' C'. (2 marks)
(c) A' B' C' undergoes a reflection along the line X = 0, obtain the coordinates and plot on the graph points A" B" C", under the transformation (2 marks)
(d) The triangle A" B" C" , undergoes an enlargement scale factor -1, centre origin. Obtain the coordinates of the image A'" B"' C"'. (2 marks)
(e) The triangle A"' B"' C"' undergoes a rotation centre (1, -2) angle 120°. Obtain the coordinates of the image #A^(iv) B^(iv) C^(iv)#. (2 marks)
(f) Which triangles are directly congruent. (1 mark)
19.The income tax rates in a certain year are as shown below.
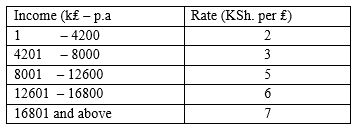
Omar pays Sh. 4000 as P.A.Y.E per month. He has a monthly house allowance of KSh.10800 and is entitled to a personal relief of KSh. 1,100 per month. Determine:
(i) his gross tax per annum in Kshs (2 Marks)
(ii) his taxable income in K₤ per annum (2 marks)
(iii) his basic salary in Ksh. per month (2marks)
(iv) his net salary per month (2 marks)
20.The diagram below shows two circles, centre A and B which intersect at points P and Q. Angle PAQ = 70°, angle PBQ = 40° and PA = AQ = 8cm.
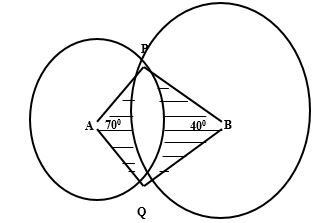
Use the diagram to calculate
(a)PQ to correct to 2 decimal places (2 Marks)
(b)PB to correct to 2 decimal places (2 Marks)
(c)Area of the minor segment of the circle whose centre is A (2 mks)
(d)Area of the minor segment of the circle whose centre is B (2mks)
(e)Area of the shaded region. (2mks)
21. Three Kenyan warships A, B and C are at sea such that ship B is 450km on a bearing of 030° from ship A. Ship C is 700km from ship B on a bearing of 120°. An enemy ship D is sighted 1000km due south of ship B.
(a) Taking a scale of 1cm to represent 100km locate the position of the ships A, B, C and D. (4 Marks)
(b)Find the compass bearing of:
(i) Ship A from ship D (1 Mark)
(ii) Ship D from ship C (1 Mark)
(c) Use the scale drawing to determine
(i) The distance of D from A (1 Mark)
(ii) The distance of C from D (1 Mark)
(d) Find the bearing of:
(i) B from C (1 Mark)
(ii) A from C (1 Mark)
22.The figure below shows triangle OPQ in which OS = #1/3# OP and OR = #1/3# OQ. T is a point on QS such that QT = #3/4# QS
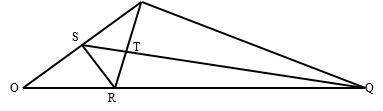
(a) Given that OP = p and OQ = q, express the following vectors in terms of p and q.
(i) SR (1 Mark)
(ii) QS (2 Marks)
(iii) PT (2 Marks)
(iv) TR (2 Marks)
(v) Show that point PTR are collinear. (3mks)
23. In the figure below DA is a diameter of the circle ABCDE centre O. TCS is a tangent to the circle at C, AB = BC and angle DAC = 38°. Giving reasons, determine the following angles:
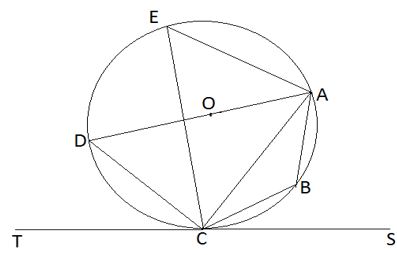
(a)#angle DCT# (2 marks)
(b)#angle DEA# (2 marks)
(c)#angle ACB# (2 marks)
(d)#angle BDC# (2 marks)
(e)#angle BOA# (2 marks)
24 (a) (i) Fill the table below for the function.
#y = 2x^2 + 5x – 12# for #-8le x le 4# (2 marks)
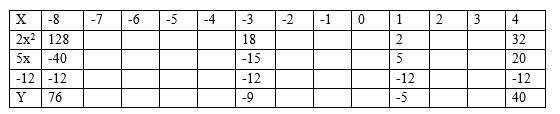
(ii) Using the table, draw the graph of the function #y = 2x^2 + 5x – 12#. Use the scale 1cm to 1 unit on the x-axis and 1cm for 10 units for the y – axis (4 marks)
b) Use the graph drawn above to solve the following equations.
(i) #2x^2 + 5x – 12 = 0 # (2 marks)
(ii) #3 – 7x – 3x^2 = 0 # (2 marks)
More Examination Papers