 Get premium membership
Get premium membership and access revision papers with marking schemes, video lessons and live classes.
Form 3 Mathematics Paper 2 End of Term 2 Exams 2021
Class: Form 3
Subject: Mathematics
Level: High School
Exam Category: Form 3 End Term 2 Exams
Document Type: Pdf
Views: 1049
Downloads: 52
Exam Summary
MATHEMATICS
PAPER 2 121/2
TIME: 2HRS
END-TERM 2 FORM 3
SECTION A (50 Marks)
Attempt all questions in the spaces provided
1. Use logarithms to evaluate. #(4.497 × sqrt0.3673)/(1- cos 81.53° ) # (3mks)
2. The sum of the fifth and sixth term of an AP is 30. If the third term is 5. Find the first term. (3mks)
3. Make K the subject of the formula and simplify. (3mks)
#t=(2y+1)/sqrt(2ky+k)#
4. Solve for x
#2-(log X )^2=3log X -log X ^2=3log X# (3mks)
5. The sides of a triangle were measured and recorded as 4cm, 6.2cm and 9.50cm.Calculate the percentage error in its perimeter correct to 2 decimal places. (3mks)
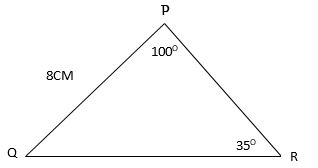
6. The figure below shows a triangle PQR in which PQ=8cm and angle QPR=100° and angle PRQ=35°.Calculate to 2 decimal places the length of QR and hence the area of triangle PQR to2 decimal places. (3mks)
7. (a) Expand #(1-2x)^6# up to term in #x^3#. (2mks)
(b) Use the expansion above to evaluate #(1.02)^6# correct to 4 decimal places. (2mks)
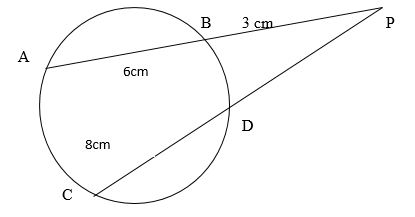
8. Find the length of DP in the figure. (3mks)
9. Given the matrix below has no inverse, find the value of x. (2mks)
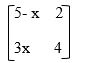
10. Without using a calculator solve #(sqrt252+sqrt72)/(sqrt(32+) sqrt28)# leaving your answer in the form #asqrt(b+c)# where a, b and c are integers. (4mks)
11. Find the radius as the center of a circle whose equation is
#3x^2 + 3y^2 + 18y -12x – 9=0# (3mks)
12. A new laptop depreciates at 8% per annum in the first year and 12% per year in the second year. If its value at the end of the second year was sh.121,440, calculate its original value. (3mks)
13. Given that C varies partly as A and partly as the square of A and that C=20 when A=2 and C=21 when A=3, determine the value of C when A=4. (3mks)
14. The size of an interior angle of a regular polygon is #6 1/2# times that of its exterior angle determine the number of sides of the polygon. (3 mks)
15. Given that the ration x : y=2:3 find the ratio (5x-2y) : (x+y). (3mks)
16. Kiprono buys tea costing sh 112 per kilogram and sh.132 per kilogram and mixes them, then sells the mixture at sh.150 per kilogram .If he is making a profit of 25% in each kilogram of the mixture, determine the ratio in which he mixes the tea. (4mks)
SECTION II
Answer ALL questions
17. Atambo poured spirit into a test tube which has hemispherical bottom of inner radius 1.5cm. He noted that the spirit is 8cm high.
(a) What is the area of surface in contact with spirit? (4mks)
(b) Calculate volume of spirit in the test tube. (4mks)
(c) If Atembo obtained the mass of the spirit as 10g. Calculate the density of the spirit. (2mks).
18. Mrs.Langat primary school head teacher earns a basic salary of sh.38,300 house allowance of sh.12,000 and radical ,allowance of sh.3,600 every month. She claims a family relief of sh.1172 and insurance relief of 10% of the premium paid. Using tax rates table below.
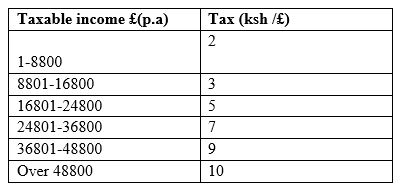
(a) Calculate Mrs.Langats annual taxable income in Kenya pound per annum. (2mks)
(b) Tax due evenly month from Mrs.Langat. (4mks)
(c) If the following deductions are made every month from her salary,
w.c p.s 2 % of basic salary
life insurance premium of sh.4 600
Sacco van repayment of sh.14, 200
Calculate
(i) the total deductions. (2mks)
(ii) Her net pay for very month. (2mk)
19. A bag contains 5 red balls, 3 blue balls and 4 yellow balls. Two balls are drawn at random one after the other without replacement.
(a)Draw a tree diagram to illustrate his pickings. (2mks )
(b) Calculate the probability that
(i) Both balls picked were red. (2mks)
(ii) Both balls picked were of the same colour. (3mks)
(c) There was no red ball from the two balls picked. (3mks)
20. In the triangle given below #vec(OP) = p# and #vec(OQ) = q#. R is a point on #vec(PQ)# such that PR: RQ = 1 : 3 and that 5OS= 2OQ. PS and OR intersect at T.
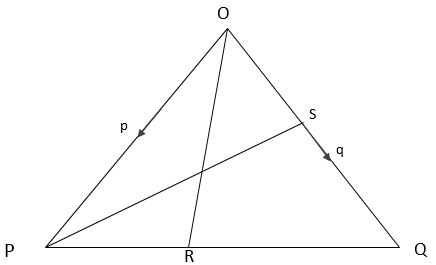
(a) Express in terms of p and q.
(i) #vec(OS)# (1mk)
(ii) #vec(PQ)# (1mk
(b)Given that OT=h OR and PT = kPS, determine the values of h and k. (6mks)
21. In the figure below,P,Q,R and S are points on the circle centre O. PRT and USTV are straight lines. Line UV is a tangent to the circle at S. #angleRST= 50°# and #angleRTV=150°#.
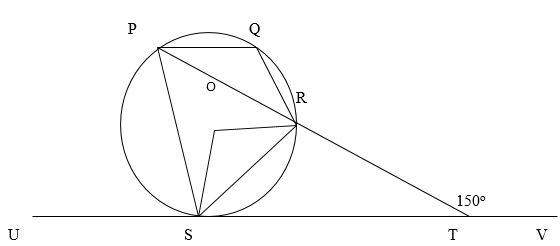
(a) Calculate the size of
(i) #angleORS # (2mks)
(ii) #angleUSP # (1mk)
(iii)#anglePQR# (2mks)
(b) Given that RT=7cm and ST=9cm,calculate to 3 significant figures
(i) Length of the line PR (2mks)
(ii)The radius of the circle. (3mks)
22. The product of the first three terms of geometric progression is 64.If the first term is a and the common ratio is r;
(a) Express r in terms of a (3mks)
(b) Given that the sum of the three terms is 14
(i)Find the values of a and r hence write down two possible sequences each up to 4th term. (5mks)
(ii)Find the sum of the first 5 terms of each sequences. (2mks)
23. (a)P, Q and R are three quantities such that P varies directly as the square of Q and inversely as the square root of R.
i) Given that P = 12 when Q = 24 and R = 36, find P when Q =27 and R = 121. (3 Marks)
ii) If Q increases by 10% and R decreases by 25%, find the percentage increase in P. (4 marks)
b) If Q is inversely proportional to the square root of P and P = 4 when Q = 3. Calculate the value of P when Q = 8. (3 marks)
24. A bus left Nairobi at 7.00 am and traveled towards Eldoret at an average speed of 80Km/hr. At 7.45am a car left Eldoret towards Nairobi at an average speed of 120Km/hr. The distance between Nairobi and Eldoret is 300 km. Calculate:
(a) The time the bus arrived at Eldoret. (2mks)
(b) The time of the day the two met. (4mks)
(c) The distance of the bus from Eldoret when the car arrived in Nairobi. (2mks)
(d) The distance from Nairobi when the two met. (2mks)
More Examination Papers