 Get premium membership
Get premium membership and access revision papers with marking schemes, video lessons and live classes.
Form 2 Mathematics End of Term 2 Exam 2021
Class: Form 2
Subject: Mathematics
Level: High School
Exam Category: Form 2 End Term 2 Exams
Document Type: Pdf
Views: 1772
Downloads: 73
Exam Summary
MATHEMATICS
TIME: 2HRS
END-TERM 2 FORM 2
SECTION A (50 Marks)
Attempt all questions in the spaces provided
1. Without using a calculator, evaluate. (3mrks)
#(-8+ (-5) times (-8)-(-6))/(-3+ (-8) ÷ 2 times 4#
2. Evaluate without using a calculator (2mrks)
#((2 3/7-1 5/6)÷5/6)/(2/3 of 2 1/4-1 1/7)#
3. In fourteen years’ time, a mother will be twice as old as her son. Four years ago, the sum of their ages was 30 years. Find how old the mother was, when the son was born. ( 4 mks)
4. A Kenya bank buys and sells foreign currencies as shown below

A tourist arrived in Kenya with 105000 Hong Kong dollars and changed the whole amount to Kenyan shillings. While in Kenya, she spent Kshs. 403,897 and changed the balance to South Africa rand before leaving for South Africa. Calculate the amount, in South African rand that she received.
(3mrks)
5 a) Using a ruler and a pair of compasses only, construct a quadrilateral PQRS in which PQ= 5cm, PS = 3cm, QR = 4cm,#anglePQR# = 135°and #angleSPQ# is a right angle. (2mrks)
b) The quadrilateral PQRS represents a plot of land drawn to a scale of 1:4000. Determine the actual length of RS in meters. (2mrks)
6. The ratio of goats to cows in a farm is 2:5 while the ratio of sheep to cows is 3:4. If there are 15 sheep, how many animals are there in farm. (2mrks)
7. Mr. Maina who deals in electronics sells a radio to a customer at Ksh. 1440 after giving a discount 0f 10% but find that he makes a 20% profit. Find the profit Mr. Maina would make if he does not give a discount. (3mrks)
8. use the reciprocal and square table to evaluate to four significant figure, the expression.(3mrks)
#1/0.03654- 4.151^2#
9. Simplify the following expression completely. (3mrks)
#((12a)^2-(3b)^2)/(2a^2-ab-b^2 )#
10. Given that sin (x + 60) ° = Cos (2x) °, find tan (x + 60) °. (3mrks)
11. The figure below shows triangle PQR in which PR = 12 cm, T is a point on PR such that TR = 4cm. line ST is Parallel to QR
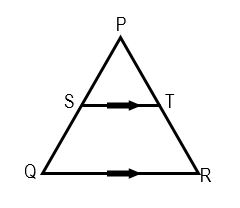
If the area of triangle PQR is 336 #cm^2#, find the area of the quadrilateral QRTS. (3mrks)
12. A square brass plate is 2 mm thick and has a mass of 1.05 kg. The density of the brass is 8.4 g/#cm^3#. Calculate the length of the plate in centimeters (3 mks)
13. The diagram below represent a solid made up of a hemisphere mounted on a cone. The common radius is 6 cm and the height of the solid is 15cm.
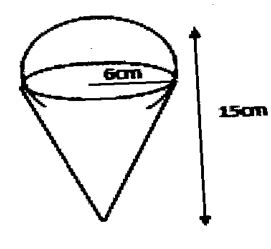
Calculate the external surface of the solid (4 Mrks)
14. Solve the simultaneous inequalities given below and list all the integral values of x (3mks)
#(3-x)/2ge(x+1)/3ge(2x+1)/(-3)#
15. A construction company employs technicians and artisans. On a certain 3 technicians and 2 artisans were hired and paid a total of Ksh9000. On another day the firm hired 4 technicians and one artisan and paid a total of Ksh 9500. Calculate the cost of hiring two technicians and 5 artisans in a day
16. The figure below is not drawn to scale. #angle QRS = 80°#
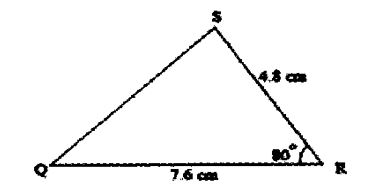
Find correct to 1 decimal place;
(a) Length PQ. (2 mark).
(b) Angle ABC (2 mark)
SECTION II (50 marks)
Answer ALL questions in this section
17. Two lines #L_1#: 2y - 3x - 6 = 0 and #L_2#: 3y+x-20 = 0 intersect at point A.
(a) Find the coordinates of A. (3 Mrks)
(b) A third line #L_3# is perpendicular to #L_2# at point A. Find the equation of #L_3# in the form y = mx +c, where m and c are constants. (3 mark)
(c) Another #L_4# is parallel to #L_1# and passes through (-1, 3). Find the x and y intercepts of #L_4#. (4 mark)
18. Town B is 180km on a bearing 0500 from town A. Another town C is on a bearing of 110° from town A and on a bearing of 150° from town B. A fourth town D is 240 km on a bearing of 320° from A. Using scale drawing, such that 1cm rep 30km,
(a) Show the relative position of the towns (4 mks)
(b) Using the diagram, find
(i) Distance AC (2 mrks)
(ii) Distance CD (2 mrks)
(iii) Compass bearing of C from D (2 mrks)
19. The figure below shows a triangle ABC inscribed in a circle. AC = 10cm, BC = 7cm and AB = 10cm.
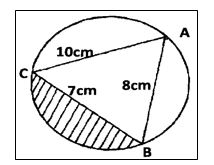
(a) Find the size of angle BAC. (3 Mks)
(b) Find the radius of the circle. (2 Mks)
(c) Hence calculate the area of the shaded region. (5 Mks)
20. The figure below represents a speed time graph for a cheetah which covered 825m in 40 seconds.
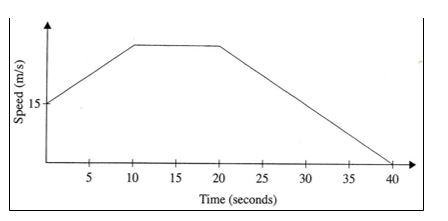
a) State the speed of the cheetah when recording of its motion started (1 mk)
b) Calculate the maximum speed attained by the cheetah (3mks)
c) Calculate the acceleration of the cheetah in:
(i) The first 10 seconds (2mks)
(ii)The last 20 seconds (1mk)
d) Calculate the average speed of the cheetah in first 20 seconds (3mks)
21. The diagram represents a solid frustum with base radius 21cm and top radius 14cm. The frustum is 22.5cm high and is made of a metal whose density is 3 g/#cm^3.(Take pi=22/7)#
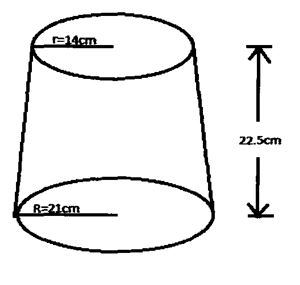
a) Calculate
(i) The volume of the metal in the frustum. (5 marks)
(ii) The mass of the frustum in kg. (2 marks)
b) The frustum is melted down and recast into a solid cube. In the process 20% of the metal is lost. Calculate to 2 decimal places the length of each side of the cube.
(3 marks)
More Examination Papers