 Get premium membership
Get premium membership and access revision papers with marking schemes, video lessons and live classes.
Form 3 Mathematics Paper 1 End of Term 3 Exams 2021
Class: Form 3
Subject: Mathematics
Level: High School
Exam Category: Form 3 End Term 3 Exams
Document Type: Pdf
Views: 820
Downloads: 65
Exam Summary
Attempt ALL the questions in the spaces provided
1. Without using a calculator, evaluate (3 marks)
#(-9+(-7)times(-8)-(-5))/(-2+(-6)div3times6)#
2. Use logarithms to evaluate (4 marks)
#34.33/sqrt(5.25times0.04#
3. Solve the equation below. (3 marks)
#(2x+5)/3 - (6-2x)/2 =2#
4. Given Sin (90 – a) = #1/2# , find without using tables or calculators the value of Cos a. (3 marks)
5. Find all the integers satisfying the inequalities. (3 marks)
#3-2x < x - 3 <=4 #
6. A number n is such that when it is divided by 27, 30 or 45, the remainder is always 3. Find the smallest value of n. (3 marks)
7. The interior angle of a n-sided regular polygon exceeds its exterior angle by 135°. Find the value of n. (3 marks)
8. Simplify the expression (3 marks)
#(9x^2 - 25y^2)/(6x^2 +19xy +15y^2)#
9. The equation of a straight line is given by 2y +8x – 10 = 0. Another line L2 cuts L1 at right angles such that the point of intersection of the two lines is (-3, K)
(a) Find the value of K (1 mk)
(b) Determine the equation of L2 in the form y = mx +c
10.The ratio of goats to cows in a farm is 2:5 while the ratio of sheep to cows is 3:4. If there are 15 sheep, how many animals are there in the farm (3 mks)
11. Mr. Maina who deals in electronics sells a radio to a customer at Ksh. 1440 after giving him a discount of 10% but find that he still makes a 20% profit. Find the profit Mr. Maina would make if he does not give a discount.(4mks)
12. The diagram below represents a solid made up of a hemisphere mounted on a cone. The common radius is 6cm and the height of the solid is 15cm.
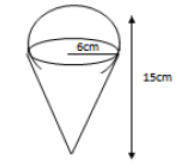
Calculate the external surface area of the solid (4mks)
13. The figure below shows triangle PQR in which PR = 12cm, T is a point on PR such that TR = 4cm.
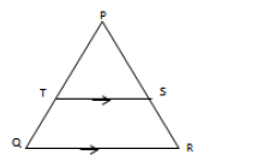
Line ST is parallel to QR. If the area of triangle PQR is 336cm2, find the area of the quadrilateral QRTS (3 mks)
14. The figure below shows a square based pyramid on top of a cuboid
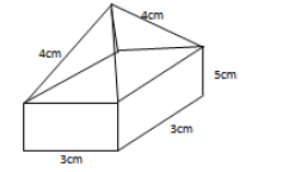
a).Draw the net of the solid (2 mks)
b) Calculate the total surface area of the net. (2 mks)
15. The difference between two positive integers is 5 and the sum of their squares is 73. Find the integers. (4 marks)
16. A cold water tap can fill a bath in 10minutes, while a hot water tap can fills it in 8 minutes. The drainage pipe can empty it in 5 minutes. The cold water and hot water taps are opened for 4 minutes. Thereafter, all the three taps are opened. Find how long it takes to fill the bath. (3marks)
SECTION 2 (50 MARKS)
Answer ANY 5 questions from this section.
17. Karanja and Kamau decided to start a business. Karanja contributed ksh.400, 000 and Kamau ksh.640, 000. The two men agreed that in any year 15% of the profit shall be divided equally between them and 20% of the profit will be used to meet the cost of the business and the rest to be shared in the ratio of their contributions. The profit made after the first year was ksh.432, 000.
a) How much did they set aside towards the cost of running the business for the 2nd year? (2mks)
b) How much did Kamau receive at the end of the first year? (4mks)
c) Karanja bought Samsung T.V sets with his share of the profit. If each T.V set cost ksh.18, 000, how many sets did he buy? (4marks).
18. The football team in school decided to raise ksh.3,600 for a party. Each student was to contribute the same amount. However, before the contributions were made, five members of the football team decided to transfer to other schools. This meant that the remaining contributors had to pay more to meet the same target.
a) If the increase in contributor per student was ksh.24. Taking the original number of footballers to be x.
i) Give an expression for the initial amount that each student should have contributed. (1mk)
ii) Give an expression for the contribution by each student after the transfer. (1mk)
iii) Form an equation hence find the number of members in the football team originally. (5mks)
iv) Calculate the percentage increase in the contribution per student caused by the transfer. (3mks)
19. A bus left Kisumu for Nairobi at an average speed of 60km/h. After 112 hours another car left Kisumu for Nairobi along the same route at an average speed of 100km/h. If the distance between Kisumu and Nairobi is 500km,determine.
a. i) The distance of the bus from Nairobi when the car took off. (2mks)
ii) The distance the car travelled to catch up with the bus. (4mks)
b) Immediately the car caught up with the bus, the car stopped for 25minutes. Find the new average speed of which the car travelled in order to reach Nairobi us the same time at the bus. (4mks)
20. A line L1 passes through the points (−2, 3) and (−1, 6) and is perpendicular to L2 at (−1, 6). a) Find the equation of 𝐿1. (2 marks)
b) Find the equation of 𝐿2 in the form 𝑎𝑥 + 𝑏𝑦 − 𝑐 = 0 where a, b and c are constants. (2 marks)
c) Given that another line 𝐿3 is parallel to 𝐿1 and passes through point (1,2) , find the 𝑥 and 𝑦 intercepts of 𝐿3 . (3 marks) d) Find the point of intersection of 𝐿2 and 𝐿3. (3 marks)
21. (a) The ratio of Juma’s and Akinyi’s earnings was 5:3. Juma’s earnings rose to Ksh 8 400 after an increase of 12%. Calculate the percentage increase in Akinyi’s earnings given that the sum of their earnings was Ksh. 14 100 (6 marks)
(b) Juma and Akinyi contributed all the new earnings to buy maize at Ksh 1 175 per bag. The maize was then sold at ksh 1 762.50 per bag. The two shared all the money from the sales of the maize in the ratio of their contributions. Calculate the amount that Akinyi got. (4 marks)
22. On the grid provided, draw the square whose vertices are (6, −2), 𝐵 (7, −2), 𝐶 (7, −1) 𝑎𝑛𝑑 𝐷 (6, −1).

(b) On the same grid, draw:
(i) 𝐴’𝐵’𝐶’𝐷’ the image of ABCD, under an enlargement scale factor 3 centre (9, −4) (3 marks)
(ii) 𝐴’’𝐵”𝐶”𝐷” the image of 𝐴’𝐵’𝐶’𝐷’ under a reflection in the line 𝑥 = 0 (2 marks)
(iii) 𝐴”’𝐵’”𝐶’”𝐷’” the image of 𝐴”𝐵”𝐶”𝐷” under a rotation of +90° about (0,0). (2 marks)
(c) Describe a single transformation that maps 𝐴’𝐵’𝐶’𝐷’ onto 𝐴”’𝐵’”𝐶’”𝐷’”. (2 marks)
23. A trader bought 8 cows and 12 goats for a total of Ksh.294,000. If he had bought 1 more cows and 3 more goats he would have spend Ksh.337,500.
(a) Form two equations to represent the above information. (2 mks)
(b) Use matrix method to determine the cost of a cow and that of a goat. (4 mks)
(c) The trader sold the animals he had bought making a profit of 40% per cow and 45% per goat.
(i) Calculate the total amount of money he received. (2 mks)
(ii) Determine his profit in Kenya shillings. (2 mks)
24. Points A,B,C and D are situated on a horizontal plane such that B is 200m on a bearing of 065° from A.C is 300m on a bearing of 120° from B and D is 150m due west of C. Using 1cm to rep 50m,
(a) Draw an accurate scale drawing representing positions ABC and D. (4 mks)
(b) From your drawing, Measure the distance and bearing of (i) D from A. (2 mks)
(ii) B from D (2 mks
(c) By construction, show the shortest distance from B to line AD. (2 mks)
More Examination Papers